Draw a Fraction Circle to Model 5 6 1 6

Equivalent Fractions

Equivalent fractions can be defined as fractions that may accept different numerators and denominators but they correspond the same value. For case, ix/12 and half dozen/8 are equivalent fractions because both are equal to 3/4 when simplified.

All equivalent fractions get reduced to the same fraction in their simplest form as seen in the above example. Explore the given lesson to get a better idea of how to detect equivalent fractions and how to check if the given fractions are equivalent.

ane.	What are Equivalent Fractions?
2.	How to Find Equivalent Fractions?
iii.	How to Decide if Two Fractions are Equivalent?
four.	Equivalent Fractions Chart
5.	FAQs on Equivalent Fractions

What are Equivalent Fractions?

Ii or more fractions are said to be equivalent if they are equal to the same fraction when simplified. For example, the equivalent fractions of 1/5 are v/25, half-dozen/xxx, and 4/twenty, which on simplification, result in the same fraction, that is, 1/v.

Equivalent Fractions Definition

Equivalent fractions are defined as those fractions which are equal to the aforementioned value irrespective of their numerators and denominators. For example, both 6/12 and iv/8 are equal to 1/2, when simplified, which means they are equivalent in nature.

Equivalent Fractions Examples

Here are some examples of equivalent fractions.

Case: 1/ii, 2/four, 3/6, and four/8 are equivalent fractions. Let us see how their values are equal. We will represent each of these fractions as circles with shaded parts. It tin can exist seen that the shaded parts in all the figures represent the same portion if seen every bit a whole.

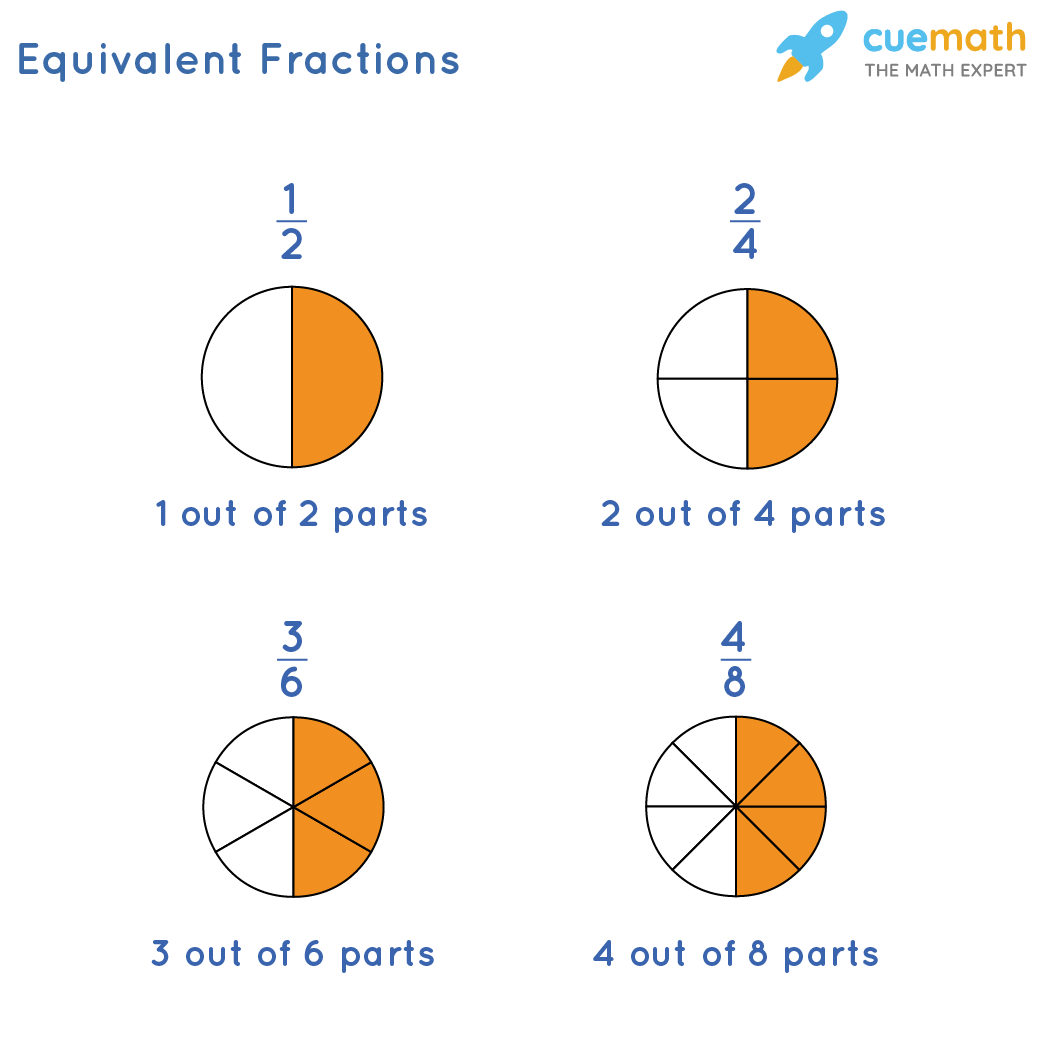
Here, we tin can come across that the amount of shaded portion is the same in all the circles. Hence, ane/2, 2/4, 3/half dozen, and four/viii are equivalent fractions.

How to Find Equivalent Fractions?

Equivalent fractions can be written by multiplying or dividing both the numerator and the denominator by the aforementioned number. This is the reason why these fractions get reduced to the same number when they are simplified. Permit us empathize the two ways in which nosotros can make equivalent fractions:

• Multiply the numerator and the denominator by the aforementioned number.
• Divide the numerator and the denominator by the same number.

Multiply the Numerator and Denominator past the Same Number

To observe the equivalent fractions for any given fraction, multiply the numerator and the denominator by the same number. For example, to find an equivalent fraction of iii/four, multiply the numerator iii and the denominator four by the same number, say, ii. Thus, 6/8 is an equivalent fraction of three/4. We can discover some other equivalent fractions by multiplying the numerator and the denominator of the given fraction by the same number.

• 3/4= \(\dfrac{3 \times 3}{4 \times 3}\) =9/12
• 3/4=\(\dfrac{3 \times four}{iv \times iv}\) =12/16
• iii/4=\(\dfrac{3 \times 5}{4 \times 5}\) =15/twenty

Thus, the equivalent fractions of three/4 are 6/eight, 9/12, 12/16, and fifteen/20.

Divide the Numerator and Denominator by the Same Number

To notice the equivalent fractions for any given fraction, divide the numerator and the denominator by the same number. For example, to find an equivalent fraction of 72/108, we volition commencement find their mutual factors. Nosotros know that two is a common gene of both 72 and 108. Hence, an equivalent fraction of 72/108 can be found by dividing its numerator and denominator past ii. Thus, 36/54 is an equivalent fraction of 72/108. Let u.s. encounter how the fraction is further simplified:

• 2 is a common factor of 36 and 54. Thus, 36/54= \(\dfrac{36 \div 2}{54 \div ii}\)= 18/27
• Again, 3 is a mutual factor of xviii and 27. Thus, 18/27= \(\dfrac{18 \div 3}{27 \div 3}\)= half-dozen/ix
• Again, 3 is a common factor of vi and nine. Thus, vi/9=\(\dfrac{6 \div 3}{nine \div 3}\)= 2/3

Therefore, a few equivalent fractions of 72/108 are 36/54, xviii/27, 6/ix, and ii/3. Here, ii/3 is the simplified form of 72/108 as there is no common factor (other than 1) of two and 3.

How to Determine if Two Fractions are Equivalent?

We demand to simplify the given fractions to find whether they are equivalent or not. Simplification to get equivalent numbers tin can exist done to a bespeak where both the numerator and denominator should still be whole numbers. There are various methods to place if the given fractions are equivalent. Some of them are:

• Making the denominators the aforementioned.
• Finding the decimal form of both the fractions.
• Cantankerous multiplication method.
• Visual method.

Let united states of america identify whether 2/vi and 3/ix are equivalent fractions by each of these methods.

Making the Denominators the Same

The denominators of the fractions, 2/6 and 3/nine are 6 and 9. The To the lowest degree Common Multiple (LCM) of the denominators 6 and ix is 18. Let us make the denominators of both fractions 18, by multiplying them with suitable numbers.

• 2/6=\(\dfrac{2 \times 3}{6 \times three}\)= half-dozen/eighteen
• 3/nine=\(\dfrac{iii \times two}{nine \times 2}\)= half-dozen/18

We can observe that both the fractions are equivalent to the same fraction 6/18. Thus, the given fractions are equivalent.

Note: If the fractions are Non equivalent, we tin can check the greater or smaller fraction by looking at the numerator of both the resultant fractions. Hence, this method can too be used for comparing fractions.

Finding the Decimal form of Both the Fractions

Let us find the decimal grade of both the fractions ii/6 and three/9 to come across if they give the same value.

• ii/half-dozen= 0.3333333...
• 3/ix= 0.3333333...

The decimal values of both the fractions are the same and hence, they are equivalent.

Cross Multiplication Method

To identify whether 2/6 and 3/9 are equivalent, we cross multiply them. If both the products are the same, the fractions are equivalent.

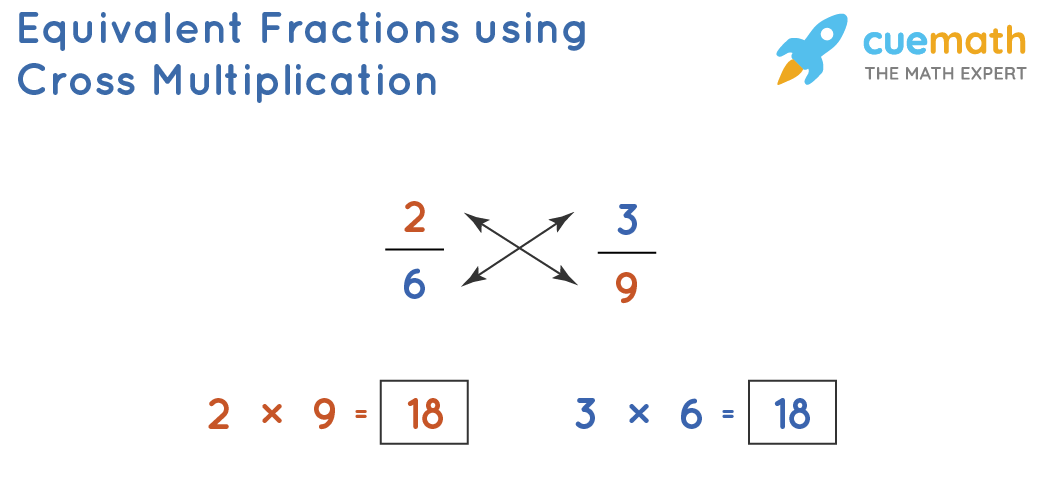
Since both the products hither are 18, the given fractions are equivalent.

Visual Method

Let us represent each of the fractions ii/6 and 3/9 pictorially on identical shapes and check if the shaded portions of both are equal.

We can run into that the shaded portions of both the circles depict the same value. In other words, it tin be seen that the shaded parts in both the figures stand for the same portion if seen as a whole. Hence, the given fractions are equivalent.

Equivalent Fractions Nautical chart

Charts and tables are often used to represent concepts in a improve way since they serve as a handy reference for calculations and are easier to empathize. Ballast charts and tables, like the one given below, brand it easier for the students to understand equivalent fractions. Allow us use the following chart to find the equivalent fractions of one/iv.

From this nautical chart, we can observe that the equivalent fractions of one/4 are: 2/8, 3/12, 4/sixteen,...

Tips on Equivalent Fractions

• Two fractions are said to be equivalent if their values (decimal/graphical) are the same.
• We usually multiply the numerator and denominator of a fraction by the same number to get its equivalent fraction.
• The 'Cross multiplication method' is used to determine whether any two fractions are equivalent or not.
• 'Making the denominators the aforementioned' is some other method used to determine if two or more fractions are equivalent.

☛ Related Manufactures

• Reduce Fractions
• Multiplying Fractions
• Improver of Fractions
• Division of Fractions
• Simplifying Fractions
• Proper Fractions

Equivalent Fractions Examples

1. Case ane: Are 12/20 and 22/30 equivalent fractions?

   Solution:

   Method 1:

   To bank check if the given fractions are equivalent, we will make the denominators the same past multiplication. The denominators of the fractions 12/20 and 22/thirty are 20 and thirty. The LCM of the denominators is threescore. Permit united states of america make the denominators of both the fractions equal to 60, by multiplying them with the suitable numbers: 12/20=\(\dfrac{12 \times iii}{20 \times three}\)= 36/60, 22/30=\(\dfrac{22 \times 2}{xxx \times 2}\)= 44/60. Here, it can exist seen that 36 is non equal to 44, that is 36 < 44. Therefore, 12/20 and 22/thirty are not equivalent fractions.

   Method 2:

   This tin can be checked by the cross multiplication method. If nosotros cross multiply the given fractions, nosotros will get twenty × 22 = 440, and 12 × thirty = 360. We can run into that 440 is not equal to 360. Therefore, 12/twenty and 22/30 are not equivalent fractions.

2. Case 2: If the numerator of a fraction equivalent to 9/xviii is 27, what is its denominator?

   Solution:

   We know that, ix/eighteen=27/? Here, the numerators of the two fractions are 9 and 27 respectively. At present, nosotros have to notice a number, which, when multiplied past 9 gives 27. We know that 9 × iii = 27. Hence, we multiply the numerator and the denominator of the given fraction by 3 =\(\dfrac{9 \times iii}{eighteen \times three}\)= 27/54. Therefore, the denominator of the equivalent fraction of ix/18 is 54.

3. Case three: Check whether the given fractions are equivalent or not: vii/13 and v/11

   Solution: Allow us check the equivalence of the given fractions past the cantankerous multiplication method. If we cross multiply the given fractions, nosotros volition get 13 × 5 = 65, and 7 × 11 = 77. We can see that 65 is not equal to 77. Therefore, 7/13 and 5/eleven are not equivalent fractions.

go to slidego to slidego to slide

Want to build a strong foundation in Math?

Go beyond memorizing formulas and sympathize the 'why' behind them. Experience Cuemath and get started.

Book a Free Trial Course

Exercise Questions on Equivalent Fractions

go to slidego to slide

FAQs on Equivalent Fractions

What are Equivalent Fractions in Math?

Two or more than fractions are said to exist equivalent fractions if they are equal to the aforementioned value irrespective of their numerators and denominators. For instance, ii/4 and eight/sixteen are equivalent fractions considering they get reduced to 1/2 when simplified.

What are the Examples of Equivalent Fractions?

There tin be many examples of equivalent fractions, like, 8/12 and 6/nine are equivalent fractions because they get reduced to the aforementioned fraction (2/3) when simplified. Similarly, 4/7 and 28/49 are also equivalent fractions.

How to Find Equivalent Fractions?

If the given fractions are simplified and they get reduced to a mutual fraction, and so they can exist termed as equivalent fractions. Apart from this, in that location are diverse other methods to identify whether the given fractions are equivalent or not. Some of them are:

1. Making the denominators the aforementioned.
2. By finding the decimal form of both the fractions.
3. Cross multiplication method.
4. Visual method.

What does information technology Mean when 2 Fractions are Equivalent?

When two fractions are equivalent, it means they are equal to the same value irrespective of their different numerators and denominators. In other words, when they are simplified they go reduced to the aforementioned fraction.

Why are Equivalent Fractions Important?

Equivalent fractions aid us to add, subtract, multiply, divide fractions, and compare fractions which helps us solve many real-fourth dimension problems.

What is an Equivalent Improper Fraction?

An equivalent improper fraction means an equivalent fraction in an improper grade. A fraction is said to be improper when its numerator is greater than its denominator. For example, 3/2 is an improper fraction that is equivalent to 9/6.

How to Effigy out Equivalent Fractions?

Any 2 fractions can exist considered to exist equivalent if they are equal to the same value. In that location are various methods to detect out if the fractions are equivalent. The basic method is past reducing them. If they become reduced to the same fraction they are considered to be equivalent.

How to Write Equivalent Fractions?

Equivalent fractions can be written by multiplying or dividing both the numerator and the denominator by the same number. This is the reason why these fractions get reduced to the same number when they are simplified. For case, let us write an equivalent fraction for 2/3. We volition multiply the numerator and denominator by 4 and we will go (two × 4)/(3 × 4) = 8/12. Therefore, eight/12 and 2/3 are equivalent fractions.

Give 2 Equivalent Fractions for 6/viii.

In order to write the equivalent fraction for 6/8, let us multiply the numerator and denominator past 2 and we will get (6 × 2)/(8 × 2) = 12/16. Therefore, 6/8 and 12/sixteen are equivalent fractions. Now, let us get some other equivalent fraction for 6/8, by dividing information technology by a common number, say, ii. After dividing the numerator and denominator by 2 and nosotros will get (6 ÷ ii)/(8 ÷ 2) = 3/4. Therefore, 6/viii and iii/4 are equivalent fractions.

bruntheaut.blogspot.com

Source: https://www.cuemath.com/numbers/equivalent-fractions/

Share this post