Draw 1 8th of Circle

Uncomplicated curve of Euclidean geometry

This article is nigh the shape and mathematical concept. For other uses, see Circle (disambiguation).

Circle
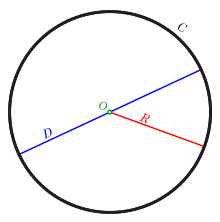A circle (black), which is measured by its circumference (C), diameter (D) in blue, and radius (R) in ruby; its centre (O) is in green.
Blazon	Conic section
Symmetry group	O(two)
Area	πR2
Perimeter	C = 2πR

A circle is a shape consisting of all points in a airplane that are at a given distance from a given point, the centre; equivalently it is the curve traced out by a bespeak that moves in a plane so that its distance from a given signal is constant. The distance between any betoken of the circumvolve and the centre is called the radius. Usually, the radius is required to be a positive number. A circle with ${\displaystyle r=0}$ is a degenerate example. This article is about circles in Euclidean geometry, and, in detail, the Euclidean plane, except where otherwise noted.

Specifically, a circle is a simple closed curve that divides the aeroplane into ii regions: an interior and an exterior. In everyday utilise, the term "circle" may be used interchangeably to refer to either the boundary of the figure, or to the whole figure including its interior; in strict technical usage, the circumvolve is only the boundary and the whole effigy is called a disc.

A circle may also be divers equally a special kind of ellipse in which the two foci are coincident, the eccentricity is 0, and the semi-major and semi-minor axes are equal; or the 2-dimensional shape enclosing the most area per unit perimeter squared, using calculus of variations.

Euclid'southward definition

A circle is a plane figure divisional past ane curved line, and such that all straight lines fatigued from a certain point inside it to the bounding line, are equal. The bounding line is called its circumference and the point, its centre.

Topological definition

In the field of topology, a circle isn't limited to the geometric concept, but to all of its homeomorphisms. Two topological circles are equivalent if ane can be transformed into the other via a deformation of R ⁱⁱⁱ upon itself (known as an ambience isotopy).^[2]

Terminology

• Annulus: a ring-shaped object, the region bounded by two concentric circles.
• Arc: any connected function of a circle. Specifying 2 cease points of an arc and a center allows for 2 arcs that together brand up a full circle.
• Centre: the betoken equidistant from all points on the circle.
• Chord: a line segment whose endpoints lie on the circle, thus dividing a circle into two segments.
• Circumference: the length of one circuit along the circle, or the distance effectually the circle.
• Diameter: a line segment whose endpoints lie on the circle and that passes through the centre; or the length of such a line segment. This is the largest altitude betwixt whatever 2 points on the circle. It is a special case of a chord, namely the longest chord for a given circle, and its length is twice the length of a radius.
• Disc: the region of the airplane bounded past a circumvolve.
• Lens: the region common to (the intersection of) two overlapping discs.
• Passant: a coplanar direct line that has no point in common with the circumvolve.
• Radius: a line segment joining the centre of a circle with any unmarried signal on the circle itself; or the length of such a segment, which is half (the length of) a diameter.
• Sector: a region divisional by two radii of equal length with a mutual heart and either of the two possible arcs, determined by this eye and the endpoints of the radii.
• Segment: a region divisional past a chord and one of the arcs connecting the chord'southward endpoints. The length of the chord imposes a lower boundary on the diameter of possible arcs. Sometimes the term segment is used only for regions non containing the eye of the circle to which their arc belongs to.
• Secant: an extended chord, a coplanar straight line, intersecting a circumvolve in two points.
• Semicircle: i of the two possible arcs determined by the endpoints of a diameter, taking its midpoint as heart. In not-technical common usage it may mean the interior of the two dimensional region divisional by a bore and i of its arcs, that is technically called a half-disc. A half-disc is a special case of a segment, namely the largest one.
• Tangent: a coplanar straight line that has one unmarried bespeak in common with a circle ("touches the circumvolve at this signal").

All of the specified regions may be considered every bit open, that is, not containing their boundaries, or equally closed, including their respective boundaries.

Chord, secant, tangent, radius, and diameter

History

The compass in this 13th-century manuscript is a symbol of God'south deed of Creation. Discover also the circular shape of the halo.

The discussion circle derives from the Greek κίρκος/κύκλος (kirkos/kuklos), itself a metathesis of the Homeric Greek κρίκος (krikos), meaning "hoop" or "ring".^[3] The origins of the words circus and excursion are closely related.

Circular slice of silk with Mongol images

The circle has been known since before the commencement of recorded history. Natural circles would accept been observed, such as the Moon, Sun, and a short establish stalk blowing in the current of air on sand, which forms a circumvolve shape in the sand. The circle is the basis for the wheel, which, with related inventions such every bit gears, makes much of modern mechanism possible. In mathematics, the study of the circumvolve has helped inspire the development of geometry, astronomy and calculus.

Early scientific discipline, particularly geometry and star divination and astronomy, was connected to the divine for most medieval scholars, and many believed that there was something intrinsically "divine" or "perfect" that could be found in circles.^{[iv] [5]}

Some highlights in the history of the circle are:

• 1700 BCE – The Rhind papyrus gives a method to find the area of a circular field. The effect corresponds to 256 / 81 (3.16049...) equally an judge value of π.^[vi]

• 300 BCE – Book 3 of Euclid's Elements deals with the backdrop of circles.
• In Plato'due south Seventh Letter in that location is a detailed definition and explanation of the circumvolve. Plato explains the perfect circle, and how it is different from any cartoon, words, definition or explanation.
• 1880 CE – Lindemann proves that π is transcendental, effectively settling the millennia-old problem of squaring the circle.^[7]

Analytic results

Circumference

The ratio of a circle's circumference to its diameter is π (pi), an irrational constant approximately equal to 3.141592654. Thus the circumference C is related to the radius r and diameter d by:

${\displaystyle C=2\pi r=\pi d.\,}$

Expanse enclosed

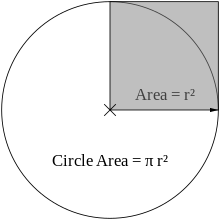
Area enclosed past a circle = π × expanse of the shaded square

As proved by Archimedes, in his Measurement of a Circle, the area enclosed by a circle is equal to that of a triangle whose base has the length of the circle's circumference and whose height equals the circle'due south radius,^[8] which comes to π multiplied by the radius squared:

${\displaystyle \mathrm {Expanse} =\pi r^{2}.\,}$

Equivalently, cogent diameter by d,

${\displaystyle \mathrm {Area} ={\frac {\pi d^{ii}}{4}}\approx 0{.}7854d^{2},}$

that is, approximately 79% of the circumscribing square (whose side is of length d).

The circle is the plane curve enclosing the maximum surface area for a given arc length. This relates the circle to a problem in the calculus of variations, namely the isoperimetric inequality.

Equations

Cartesian coordinates

Circle of radius r = one, centre (a,b) = (1.2, −0.v)

Equation of a circle

In an ten–y Cartesian coordinate system, the circle with heart coordinates (a, b) and radius r is the set of all points (ten, y) such that

${\displaystyle (x-a)^{2}+(y-b)^{2}=r^{ii}.}$

This equation, known as the equation of the circumvolve, follows from the Pythagorean theorem applied to any point on the circle: every bit shown in the next diagram, the radius is the hypotenuse of a right-angled triangle whose other sides are of length |x − a| and |y − b|. If the circle is centred at the origin (0, 0), then the equation simplifies to

${\displaystyle x^{two}+y^{2}=r^{ii}.}$

Parametric form

The equation tin can be written in parametric form using the trigonometric functions sine and cosine as

${\displaystyle x=a+r\,\cos t,}$

${\displaystyle y=b+r\,\sin t,}$

where t is a parametric variable in the range 0 to twoπ, interpreted geometrically every bit the angle that the ray from (a,b) to (x,y) makes with the positive 10 centrality.

An alternative parametrisation of the circle is

${\displaystyle x=a+r{\frac {i-t^{2}}{1+t^{2}}},}$

${\displaystyle y=b+r{\frac {2t}{1+t^{2}}}.}$

In this parameterisation, the ratio of t to r tin can be interpreted geometrically equally the stereographic project of the line passing through the centre parallel to the x axis (see Tangent half-angle substitution). However, this parameterisation works only if t is made to range not merely through all reals but besides to a point at infinity; otherwise, the leftmost point of the circumvolve would be omitted.

three-signal form

The equation of the circle determined by three points ${\displaystyle (x_{1},y_{ane}),(x_{2},y_{2}),(x_{3},y_{three})}$ non on a line is obtained past a conversion of the 3-point form of a circle equation:

${\displaystyle {\frac {({\color {dark-green}x}-x_{one})({\color {green}ten}-x_{2})+({\color {red}y}-y_{ane})({\color {carmine}y}-y_{two})}{({\color {ruby-red}y}-y_{1})({\colour {green}x}-x_{2})-({\color {cerise}y}-y_{2})({\colour {greenish}ten}-x_{one})}}={\frac {(x_{3}-x_{1})(x_{3}-x_{2})+(y_{3}-y_{1})(y_{iii}-y_{2})}{(y_{3}-y_{1})(x_{3}-x_{2})-(y_{3}-y_{2})(x_{3}-x_{one})}}.}$

Homogeneous class

In homogeneous coordinates, each conic section with the equation of a circle has the form

${\displaystyle ten^{ii}+y^{ii}-2axz-2byz+cz^{2}=0.}$

Information technology tin can be proven that a conic section is a circumvolve exactly when it contains (when extended to the circuitous projective airplane) the points I(1: i: 0) and J(1: −i: 0). These points are called the circular points at infinity.

Polar coordinates

In polar coordinates, the equation of a circle is

${\displaystyle r^{2}-2rr_{0}\cos(\theta -\phi )+r_{0}^{2}=a^{two},}$

where a is the radius of the circle, ${\displaystyle (r,\theta )}$ are the polar coordinates of a generic betoken on the circle, and ${\displaystyle (r_{0},\phi )}$ are the polar coordinates of the middle of the circle (i.e., r ₀ is the distance from the origin to the centre of the circle, and φ is the anticlockwise angle from the positive 10 axis to the line connecting the origin to the centre of the circle). For a circumvolve centred on the origin, i.e. r ₀ = 0, this reduces to simply r = a . When r ₀ = a , or when the origin lies on the circle, the equation becomes

${\displaystyle r=2a\cos(\theta -\phi ).}$

In the general example, the equation can be solved for r, giving

${\displaystyle r=r_{0}\cos(\theta -\phi )\pm {\sqrt {a^{2}-r_{0}^{2}\sin ^{two}(\theta -\phi )}}.}$

Note that without the ± sign, the equation would in some cases depict only half a circle.

Complex plane

In the complex plane, a circumvolve with a centre at c and radius r has the equation

${\displaystyle |z-c|=r.}$

In parametric form, this tin be written as

${\displaystyle z=re^{it}+c.}$

The slightly generalised equation

${\displaystyle pz{\overline {z}}+gz+{\overline {gz}}=q}$

for real p, q and circuitous g is sometimes called a generalised circle. This becomes the above equation for a circumvolve with ${\displaystyle p=i,\ m=-{\overline {c}},\ q=r^{2}-|c|^{two}}$ , since ${\displaystyle |z-c|^{2}=z{\overline {z}}-{\overline {c}}z-c{\overline {z}}+c{\overline {c}}}$ . Not all generalised circles are really circles: a generalised circle is either a (truthful) circle or a line.

Tangent lines

The tangent line through a point P on the circumvolve is perpendicular to the bore passing through P. If P = (x ₁, y ₁) and the circumvolve has centre (a, b) and radius r, then the tangent line is perpendicular to the line from (a, b) to (10 ₁, y ₁), so it has the form (x ₁ − a)x + (y _one – b)y = c . Evaluating at (ten _i, y ₁) determines the value of c, and the result is that the equation of the tangent is

${\displaystyle (x_{ane}-a)x+(y_{i}-b)y=(x_{1}-a)x_{1}+(y_{1}-b)y_{ane},}$

or

${\displaystyle (x_{1}-a)(10-a)+(y_{1}-b)(y-b)=r^{two}.}$

If y ₁ ≠ b , then the gradient of this line is

${\displaystyle {\frac {dy}{dx}}=-{\frac {x_{1}-a}{y_{i}-b}}.}$

This can likewise be institute using implicit differentiation.

When the centre of the circle is at the origin, and then the equation of the tangent line becomes

${\displaystyle x_{1}x+y_{1}y=r^{two},}$

and its slope is

${\displaystyle {\frac {dy}{dx}}=-{\frac {x_{i}}{y_{1}}}.}$

Properties

• The circle is the shape with the largest area for a given length of perimeter (meet Isoperimetric inequality).
• The circle is a highly symmetric shape: every line through the eye forms a line of reflection symmetry, and it has rotational symmetry effectually the center for every angle. Its symmetry grouping is the orthogonal grouping O(2,R). The grouping of rotations alone is the circle group T.
• All circles are similar.
  • A circle circumference and radius are proportional.
  • The expanse enclosed and the foursquare of its radius are proportional.
  • The constants of proportionality are 2π and π respectively.
• The circle that is centred at the origin with radius one is called the unit of measurement circle.
  • Thought of equally a great circle of the unit sphere, it becomes the Riemannian circle.
• Through any three points, non all on the aforementioned line, there lies a unique circumvolve. In Cartesian coordinates, it is possible to give explicit formulae for the coordinates of the centre of the circle and the radius in terms of the coordinates of the iii given points. Encounter circumcircle.

Chord

• Chords are equidistant from the heart of a circle if and just if they are equal in length.
• The perpendicular bisector of a chord passes through the center of a circle; equivalent statements stemming from the uniqueness of the perpendicular bisector are:
  • A perpendicular line from the centre of a circle bisects the chord.
  • The line segment through the centre bisecting a chord is perpendicular to the chord.
• If a key bending and an inscribed angle of a circle are subtended by the same chord and on the same side of the chord, then the fundamental angle is twice the inscribed angle.
• If two angles are inscribed on the same chord and on the aforementioned side of the chord, then they are equal.
• If two angles are inscribed on the aforementioned chord and on opposite sides of the chord, then they are supplementary.
  • For a circadian quadrilateral, the exterior angle is equal to the interior opposite angle.
• An inscribed bending subtended by a bore is a right angle (see Thales' theorem).
• The diameter is the longest chord of the circumvolve.
  • Amongst all the circles with a chord AB in common, the circle with minimal radius is the i with diameter AB.
• If the intersection of any two chords divides one chord into lengths a and b and divides the other chord into lengths c and d, and so ab = cd .
• If the intersection of any two perpendicular chords divides one chord into lengths a and b and divides the other chord into lengths c and d, then a ⁱⁱ + b ^two + c ^two + d ² equals the square of the diameter.^[nine]
• The sum of the squared lengths of any 2 chords intersecting at right angles at a given point is the aforementioned as that of any other two perpendicular chords intersecting at the same point and is given by 8r ² − 4p ², where r is the circle radius, and p is the distance from the centre point to the signal of intersection.^[10]
• The distance from a point on the circle to a given chord times the diameter of the circle equals the product of the distances from the bespeak to the ends of the chord.^{[xi] : p.71}

Tangent

• A line fatigued perpendicular to a radius through the end signal of the radius lying on the circle is a tangent to the circle.
• A line drawn perpendicular to a tangent through the betoken of contact with a circle passes through the eye of the circle.
• Two tangents can always be drawn to a circle from any indicate outside the circle, and these tangents are equal in length.
• If a tangent at A and a tangent at B intersect at the outside point P, then cogent the centre as O, the angles ∠BOA and ∠BPA are supplementary.
• If AD is tangent to the circle at A and if AQ is a chord of the circle, and then ∠DAQ = 1 / two arc(AQ).

Theorems

• The chord theorem states that if two chords, CD and EB, intersect at A, and so AC × Ad = AB × AE .
• If two secants, AE and Advertizing, also cutting the circle at B and C respectively, and then Air-conditioning × AD = AB × AE (corollary of the chord theorem).
• A tangent can be considered a limiting case of a secant whose ends are coincident. If a tangent from an external point A meets the circumvolve at F and a secant from the external point A meets the circumvolve at C and D respectively, then AF ² = AC × AD (tangent–secant theorem).
• The angle betwixt a chord and the tangent at 1 of its endpoints is equal to one one-half the angle subtended at the middle of the circle, on the contrary side of the chord (tangent chord angle).
• If the angle subtended by the chord at the centre is ninety°, then ℓ = r √two , where ℓ is the length of the chord, and r is the radius of the circle.
• If ii secants are inscribed in the circumvolve as shown at right, then the measurement of angle A is equal to one half the difference of the measurements of the enclosed arcs ( ${\displaystyle {\overset {\frown }{DE}}}$ and ${\displaystyle {\overset {\frown }{BC}}}$ ). That is, ${\displaystyle two\bending {CAB}=\angle {DOE}-\angle {BOC}}$ , where O is the centre of the circle (secant–secant theorem).

Inscribed angles

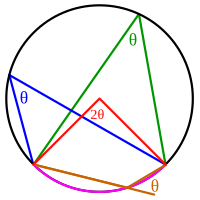
An inscribed angle (examples are the blueish and green angles in the figure) is exactly half the corresponding key angle (reddish). Hence, all inscribed angles that subtend the same arc (pink) are equal. Angles inscribed on the arc (brown) are supplementary. In detail, every inscribed angle that subtends a diameter is a right angle (since the central bending is 180°).

Sagitta

The sagitta is the vertical segment.

The sagitta (also known as the versine) is a line segment drawn perpendicular to a chord, between the midpoint of that chord and the arc of the circle.

Given the length y of a chord and the length ten of the sagitta, the Pythagorean theorem tin can be used to summate the radius of the unique circle that will fit around the 2 lines:

${\displaystyle r={\frac {y^{ii}}{8x}}+{\frac {x}{2}}.}$

Another proof of this result, which relies only on ii chord properties given to a higher place, is every bit follows. Given a chord of length y and with sagitta of length x, since the sagitta intersects the midpoint of the chord, nosotros know that information technology is a part of a diameter of the circle. Since the bore is twice the radius, the "missing" function of the bore is (iir − x ) in length. Using the fact that ane part of one chord times the other part is equal to the same product taken along a chord intersecting the first chord, we find that (2r − x)x = (y / 2)² . Solving for r, we find the required upshot.

Compass and straightedge constructions

There are many compass-and-straightedge constructions resulting in circles.

The simplest and nigh basic is the structure given the middle of the circle and a point on the circle. Place the fixed leg of the compass on the eye signal, the movable leg on the point on the circumvolve and rotate the compass.

Construction with given diameter

• Construct the midpoint Grand of the diameter.
• Construct the circle with centre Thou passing through one of the endpoints of the diameter (it will also laissez passer through the other endpoint).

Construct a circle through points A, B and C by finding the perpendicular bisectors (red) of the sides of the triangle (bluish). Only two of the three bisectors are needed to detect the middle.

Construction through three noncollinear points

• Proper name the points P , Q and R ,
• Construct the perpendicular bisector of the segment PQ .
• Construct the perpendicular bisector of the segment PR .
• Label the point of intersection of these ii perpendicular bisectors M . (They meet because the points are not collinear).
• Construct the circumvolve with centre M passing through one of the points P , Q or R (it will besides laissez passer through the other two points).

Circle of Apollonius

Apollonius' definition of a circumvolve: d _i/d ₂ constant

Apollonius of Perga showed that a circumvolve may also be defined equally the set of points in a plane having a abiding ratio (other than ane) of distances to two stock-still foci, A and B.^{[12] [thirteen]} (The set of points where the distances are equal is the perpendicular bisector of segment AB, a line.) That circle is sometimes said to exist fatigued about 2 points.

The proof is in two parts. First, one must prove that, given 2 foci A and B and a ratio of distances, any betoken P satisfying the ratio of distances must fall on a detail circle. Let C exist some other point, likewise satisfying the ratio and lying on segment AB. By the angle bisector theorem the line segment PC will bifurcate the interior angle APB, since the segments are similar:

${\displaystyle {\frac {AP}{BP}}={\frac {AC}{BC}}.}$

Analogously, a line segment PD through some indicate D on AB extended bisects the corresponding exterior bending BPQ where Q is on AP extended. Since the interior and exterior angles sum to 180 degrees, the bending CPD is exactly 90 degrees; that is, a correct angle. The set of points P such that angle CPD is a correct angle forms a circle, of which CD is a diameter.

2d, see^{[xiv] : p.15} for a proof that every point on the indicated circumvolve satisfies the given ratio.

Cross-ratios

A closely related property of circles involves the geometry of the cross-ratio of points in the circuitous airplane. If A, B, and C are as above, and so the circumvolve of Apollonius for these 3 points is the collection of points P for which the absolute value of the cross-ratio is equal to one:

${\displaystyle {\big |}[A,B;C,P]{\big |}=1.}$

Stated another way, P is a betoken on the circle of Apollonius if and only if the cross-ratio [A, B; C, P] is on the unit circle in the circuitous airplane.

Generalised circles

If C is the midpoint of the segment AB, then the collection of points P satisfying the Apollonius condition

${\displaystyle {\frac {|AP|}{|BP|}}={\frac {|Air-conditioning|}{|BC|}}}$

is non a circle, only rather a line.

Thus, if A, B, and C are given singled-out points in the plane, then the locus of points P satisfying the to a higher place equation is chosen a "generalised circumvolve." Information technology may either be a true circle or a line. In this sense a line is a generalised circumvolve of space radius.

Inscription in or circumscription about other figures

In every triangle a unique circle, chosen the incircle, can be inscribed such that information technology is tangent to each of the three sides of the triangle.^[15]

About every triangle a unique circle, called the circumcircle, tin exist circumscribed such that it goes through each of the triangle's three vertices.^[16]

A tangential polygon, such as a tangential quadrilateral, is any convex polygon within which a circle can be inscribed that is tangent to each side of the polygon.^[17] Every regular polygon and every triangle is a tangential polygon.

A cyclic polygon is any convex polygon about which a circumvolve tin can be confining, passing through each vertex. A well-studied case is the cyclic quadrilateral. Every regular polygon and every triangle is a circadian polygon. A polygon that is both cyclic and tangential is called a bicentric polygon.

A hypocycloid is a curve that is inscribed in a given circle by tracing a fixed point on a smaller circle that rolls inside and tangent to the given circle.

Limiting example of other figures

The circle tin be viewed as a limiting case of each of various other figures:

• A Cartesian oval is a set of points such that a weighted sum of the distances from any of its points to ii stock-still points (foci) is a constant. An ellipse is the case in which the weights are equal. A circle is an ellipse with an eccentricity of zippo, meaning that the two foci coincide with each other as the centre of the circle. A circle is also a unlike special case of a Cartesian oval in which i of the weights is zero.
• A superellipse has an equation of the class ${\displaystyle \left|{\frac {ten}{a}}\correct|^{n}\!+\left|{\frac {y}{b}}\right|^{due north}\!=1}$ for positive a, b, and due north. A supercircle has b = a . A circle is the special case of a supercircle in which n = ii.
• A Cassini oval is a set of points such that the production of the distances from any of its points to 2 fixed points is a constant. When the 2 fixed points coincide, a circumvolve results.
• A bend of constant width is a figure whose width, defined as the perpendicular altitude between 2 distinct parallel lines each intersecting its purlieus in a unmarried bespeak, is the same regardless of the direction of those two parallel lines. The circle is the simplest example of this type of figure.

In other p-norms

Illustrations of unit circles (see also superellipse) in unlike p -norms (every vector from the origin to the unit of measurement circle has a length of one, the length beingness calculated with length-formula of the corresponding p ).

Defining a circle every bit the set of points with a stock-still distance from a bespeak, different shapes can be considered circles under different definitions of distance. In p-norm, altitude is adamant by

${\displaystyle \left\|ten\right\|_{p}=\left(|x_{1}|^{p}+|x_{2}|^{p}+\dotsb +|x_{n}|^{p}\right)^{ane/p}.}$

In Euclidean geometry, p = 2, giving the familiar

${\displaystyle \left\|x\right\|_{2}={\sqrt {|x_{1}|^{ii}+|x_{two}|^{2}+\dotsb +|x_{n}|^{2}}}.}$

In taxicab geometry, p = 1. Taxicab circles are squares with sides oriented at a 45° angle to the coordinate axes. While each side would have length ${\displaystyle {\sqrt {two}}r}$ using a Euclidean metric, where r is the circle'south radius, its length in taxicab geometry is 2r. Thus, a circle's circumference is 8r. Thus, the value of a geometric analog to ${\displaystyle \pi }$ is 4 in this geometry. The formula for the unit circle in taxicab geometry is ${\displaystyle |ten|+|y|=1}$ in Cartesian coordinates and

${\displaystyle r={\frac {1}{|\sin \theta |+|\cos \theta |}}}$

in polar coordinates.

A circle of radius 1 (using this distance) is the von Neumann neighborhood of its center.

A circle of radius r for the Chebyshev distance (Fifty_∞ metric) on a plane is also a square with side length iir parallel to the coordinate axes, and so planar Chebyshev distance tin be viewed every bit equivalent past rotation and scaling to planar taxicab distance. However, this equivalence betwixt 50₁ and L_∞ metrics does not generalize to higher dimensions.

Locus of constant sum

Consider a finite ready of ${\displaystyle n}$ points in the airplane. The locus of points such that the sum of the squares of the distances to the given points is constant is a circle, whose heart is at the centroid of the given points.^[18] A generalization for higher powers of distances is obtained if under ${\displaystyle n}$ points the vertices of the regular polygon ${\displaystyle P_{n}}$ are taken.^[19] The locus of points such that the sum of the ${\displaystyle (2m)}$ -th power of distances ${\displaystyle d_{i}}$ to the vertices of a given regular polygon with circumradius ${\displaystyle R}$ is constant is a circle, if

${\displaystyle \sum _{i=ane}^{due north}d_{i}^{2m}>nR^{2m}}$ , where ${\displaystyle m}$ =i,2,…, ${\displaystyle n}$ -1;

whose center is the centroid of the ${\displaystyle P_{north}}$ .

In the example of the equilateral triangle, the loci of the constant sums of the 2d and fourth powers are circles, whereas for the square, the loci are circles for the constant sums of the 2nd, fourth, and sixth powers. For the regular pentagon the abiding sum of the eighth powers of the distances will be added and so forth.

Squaring the circle

Squaring the circumvolve is the trouble, proposed by ancient geometers, of constructing a square with the aforementioned area as a given circle by using only a finite number of steps with compass and straightedge.

In 1882, the chore was proven to be incommunicable, as a consequence of the Lindemann–Weierstrass theorem, which proves that pi (π) is a transcendental number, rather than an algebraic irrational number; that is, it is not the root of whatever polynomial with rational coefficients. Despite the impossibility, this topic continues to exist of interest for pseudomath enthusiasts.

Significance in art and symbolism

From the fourth dimension of the earliest known civilisations – such equally the Assyrians and aboriginal Egyptians, those in the Indus Valley and along the Yellowish River in China, and the Western civilisations of aboriginal Greece and Rome during classical Antiquity – the circle has been used directly or indirectly in visual art to convey the artist's message and to express certain ideas. However, differences in worldview (beliefs and civilisation) had a smashing touch on artists' perceptions. While some emphasised the circle's perimeter to demonstrate their democratic manifestation, others focused on its heart to symbolise the concept of cosmic unity. In mystical doctrines, the circumvolve mainly symbolises the infinite and cyclical nature of being, but in religious traditions information technology represents heavenly bodies and divine spirits. The circumvolve signifies many sacred and spiritual concepts, including unity, infinity, wholeness, the universe, divinity, balance, stability and perfection, among others. Such concepts have been conveyed in cultures worldwide through the use of symbols, for instance, a compass, a halo, the vesica piscis and its derivatives (fish, eye, aureole, mandorla, etc.), the ouroboros, the Dharma wheel, a rainbow, mandalas, rose windows and then forth.^[20]

Run into also

References

1. ^ OL 7227282M
2. ^ Gamelin, Theodore (1999). Introduction to topology . Mineola, Due north.Y: Dover Publications. ISBN0486406806.
3. ^ krikos Archived 2013-11-06 at the Wayback Motorcar, Henry George Liddell, Robert Scott, A Greek-English Dictionary, on Perseus
4. ^ Arthur Koestler, The Sleepwalkers: A History of Human being'south Irresolute Vision of the Universe (1959)
5. ^ Proclus, The Half-dozen Books of Proclus, the Ideal Successor, on the Theology of Plato Archived 2017-01-23 at the Wayback Machine Tr. Thomas Taylor (1816) Vol. ii, Ch. 2, "Of Plato"
6. ^ Chronology for 30000 BC to 500 BC Archived 2008-03-22 at the Wayback Machine. History.mcs.st-andrews.ac.uk. Retrieved on 2012-05-03.
7. ^ Squaring the circumvolve Archived 2008-06-24 at the Wayback Machine. History.mcs.st-andrews.ac.uk. Retrieved on 2012-05-03.
8. ^ Katz, Victor J. (1998), A History of Mathematics / An Introduction (2nd ed.), Addison Wesley Longman, p. 108, ISBN978-0-321-01618-8
9. ^ Posamentier and Salkind, Challenging Issues in Geometry, Dover, 2nd edition, 1996: pp. 104–105, #4–23.
10. ^ Higher Mathematics Periodical 29(4), September 1998, p. 331, problem 635.
11. ^ Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ., 2007.
12. ^ Harkness, James (1898). "Introduction to the theory of analytic functions". Nature. 59 (1530): 30. Bibcode:1899Natur..59..386B. doi:ten.1038/059386a0. S2CID 4030420. Archived from the original on 2008-10-07.
13. ^ Ogilvy, C. Stanley, Excursions in Geometry, Dover, 1969, 14–17.
14. ^ Altshiller-Court, Nathan, Higher Geometry, Dover, 2007 (orig. 1952).
15. ^ Incircle – from Wolfram MathWorld Archived 2012-01-21 at the Wayback Automobile. Mathworld.wolfram.com (2012-04-26). Retrieved on 2012-05-03.
16. ^ Circumcircle – from Wolfram MathWorld Archived 2012-01-twenty at the Wayback Machine. Mathworld.wolfram.com (2012-04-26). Retrieved on 2012-05-03.
17. ^ Tangential Polygon – from Wolfram MathWorld Archived 2013-09-03 at the Wayback Auto. Mathworld.wolfram.com (2012-04-26). Retrieved on 2012-05-03.
18. ^ Apostol, Tom; Mnatsakanian, Mamikon (2003). "Sums of squares of distances in m-space". American Mathematical Monthly. 110 (6): 516–526. doi:10.1080/00029890.2003.11919989. S2CID 12641658.
19. ^ Meskhishvili, Mamuka (2020). "Circadian Averages of Regular Polygons and Platonic Solids". Communications in Mathematics and Applications. 11: 335–355. arXiv:2010.12340.
20. ^ Abdullahi, Yahya (October 29, 2019). "The Circumvolve from Due east to West". In Charnier, Jean-François (ed.). The Louvre Abu Dhabi: A World Vision of Fine art. Rizzoli International Publications, Incorporated. ISBN9782370741004.

Further reading

• Pedoe, Dan (1988). Geometry: a comprehensive course . Dover. ISBN9780486658124.
• "Circle" in The MacTutor History of Mathematics archive

External links

Wikiquote has quotations related to: Circles

• "Circle", Encyclopedia of Mathematics, Ems Press, 2001 [1994]
• Circumvolve at PlanetMath.
• Weisstein, Eric W. "Circle". MathWorld.
• "Interactive Java applets". for the properties of and unproblematic constructions involving circles
• "Interactive Standard Form Equation of Circumvolve". Click and drag points to see standard form equation in activity
• "Munching on Circles". cut-the-knot

bruntheaut.blogspot.com

Source: https://en.wikipedia.org/wiki/Circle

Share this post